Using Function Notation Describe Linear Transformation Geometrically
R n R m domain codomain T x T x range T. R n R m Lineartransformation m n matrix A C T e 1 T e 2 T e n D T.

Transformations Of Linear And Absolute Value Functions Ppt Download Absolute Value Writing Functions Parent Functions
G x f x k.

. If it is prove that it is. Matrix of a Linear Transformation If T. 1 Find the standard matrix for T.
E Give the matrix representation of a linear. F x f textbf x f x is a linear combination of these transformed vectors. Drag a point to play the role of the dependent variable as the independent variable follows a given path.
D Given the action of a transformation on each vector in a basis for a space determine the action on an arbitrary vector in the space. A Let S c be the set of di erentiable functions ux that satisfy the di erential equa-tion u0 2xu c for all real x. It may help to think of T as a machine that takes x as an input and gives you T x as the output.
F x displaystyle fleft xright f x a new function. A linear transformation is a function T. A function T.
V W is called a linear transformation of V into W if following two prper-ties are true for all uv V and scalars c. I make short to-the-point online math tutorials. 3 Show that T x 14 x for each vector x on H.
Displaystyle k k is a constant is a vertical shift of the function. Linear Transformation Lapbq aLp bLq Linesplanes transform to linesplanes If transformation of vertices are known transformation of linear combination of vertices can be achieved p and q are points or vectors in n1x1 homogeneous coordinates For 2D 3x1 homogeneous coordinates For 3D 4x1 homogeneous. 2 Show that the image range of T is the plane H.
Since rotates every vector in every nonzero vector changes direction so there are no eigenvectors in the plane. R n R m means T is a transformation from R n to R m. Describe geometrically what the linear transformation S does.
Rm Rn is a linear transformation then there is a matrix A such that Tx Ax for every x in Rm. R 3 R 3 be the transformation T x y z 13 x 2 y 3 z 10 y 2 x 6 z 5 z 3 x 6 y. B Let C2R be the linear space of all functions from R to R that have two continuous.
0 1 1 0 Provided that this transformation corresponds to the rotation clockwise by 90 degrees. It takes a vector as input and transforms it into a new output vector. Let H be the plane x 2 y 3 z 0 let N be the line N Span 1 2 3.
19 The Matrix of a Linear Transformation. Linear Transformations The two basic vector operations are addition and scaling. If it isnt give a counterexample.
Here the function Ltakes a vector in R2and transforms it into a vector in R3. Given the linear transformation R 2 R 2 with. To determine if a given transformation is linear.
Linear transformations are the same as matrix transformations which come from matrices. Since these vectors are not in we cannot see them. Restrict the domains of functions and observe the effect on the range.
Use function notation with geometric transformations. F textbf x f x is a linear combination of the transformed standard basis vectors. Let and be vector spaces and let be a linear transformation.
For example L11 121 and L26 246. Consider the vector We compute. 18 Introduction to Linear Transformations To determine the domain codomain and range of a given linear transformation.
To determine algebraically and geometrically the effect of a given linear transformation on given vectors. A linear transformation or simply transformation sometimes called linear map is a mapping between two vector spaces. We say that T preserves additivity 2.
A function is said to be linear if the properties of additivity and scalar multiplication are preserved that is the same result is obtained if these operations are done before or after. 1 Tx y Tx Ty for all xy 2Rn 2 Tcx cTx for all x 2Rn and c2R. Function notation also helps us to identify the element of a function which has to be examined.
The hope is to be able to use the tools developed thus far to describe the set of all x 2Rn satisfying a given equation Ax b. Ax 0 Solution Sets of Inhomogeneous Systems Another Perspective on Lines and Planes Some Terminology Solution Sets Now we seek to understand the solution sets of such equations. Let CR be the linear space of all continuous functions from R to R.
It sends x y to y x. All the output values change by. Definition 611 Let V and W be two vector spaces.
Displaystyle gleft xrightfleft xrightk gx f x k where. From this perspec-tive the nicest functions are those which preserve these operations. R n R m T x Ax m n matrix A.
The correspondence can be summarized in the following dictionary. It is important to pay attention to the locations of the kernel and the image. We will call A the matrix that represents the transformation.
This particular function satisfies the linearity condition below and so would be called a linear transformation from R2to R3. Quickly memorize the terms phrases and much more. Consider a linear function y 3x 7.
A function will be called a linear transformation defined as follows. The kernel of denoted by is the set In other words the kernel of consists of all vectors of that map to in. For which values of the real constant cis this set a linear subspace of CR.
Second in the new vector space the vector. To write such function in function notation we simply replace the variable y with the phrase fx to get. This is particularly useful to visualize by coloring unit squares and seeing how they are transformed.
Function notation allows to identify the independent variable with ease. It turns out that the converse of this is true as well. I struggled with math growing up and have been able to use those experiences to help students improve in ma.
But it turns out that does have eigenvectors and eigenvalues but in order to find them we need to work with vectors whose entries are complex numbers. 1 0 0 1 and T. C Determine whether a given transformation from Rm to Rn is linear.
The Kernel of a Linear Transformation. RnRm which satis es. F x displaystyle fleft xright f x.
Fx 3x 7. We already proved that is a subspace of the codomain.

Transformation Unit By Systry Translations Math Math Notebooks Math Journals

Parent Functions And Transformations She Loves Math Parent Functions Love Math Math
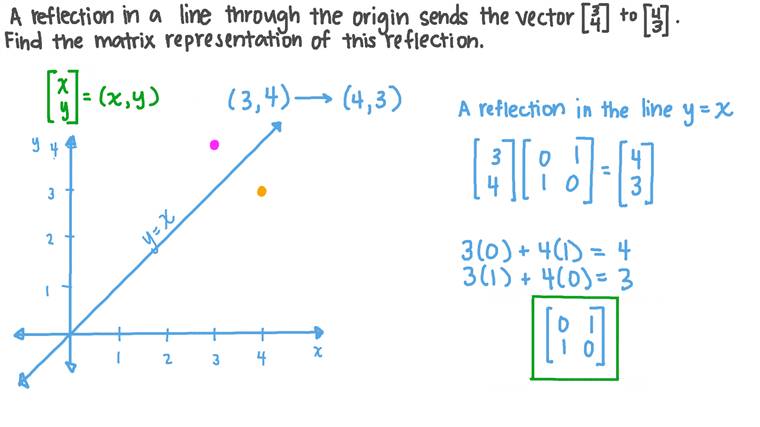
Lesson Linear Transformations In Planes Reflection Nagwa

Transformations Practice Packet 8th Grade Math Reflection Math 8th Grade Math Transformations Math

Angle Relationships Parallel Lines Teaching Geometry Studying Math Angle Relationships

Introduction To Transformations With Desmos Marbleslides This Marbleslides Activity Introduces Students To Transformation Form Using Math Blog Math Quadratics

Arithmetic And Geometric Sequence Sum Nth Term Cheat Sheet Foldable Geometric Sequences Arithmetic Foldables
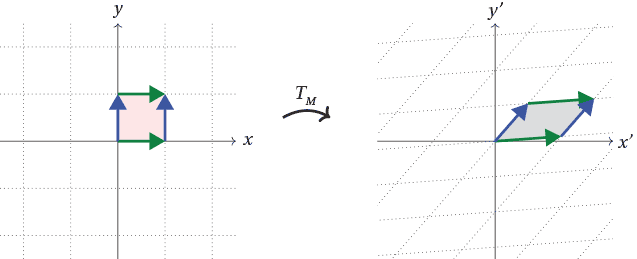
Content Linear Transformations And Matrices

2 2 Linear Transformations In Geometry For An Animation Of This Topic Visit Ppt Download

Transformations Booklet Video Transformations Math Math Resources Reflection Math
Content Describing Geometric Transformations Algebraically

Rules For Transformation Of Functions Functions Math Parent Functions Functions Algebra

Question Video Geometric Interpretation Of Linear Transformations Nagwa

Understanding One To One And Inverse Functions Inverse Functions Education Math Understanding

A Geometric Approach To Functions

Parent Functions And Transformations She Loves Math Math Lessons Studying Math Quadratics

Dynamic Transformations Using Peardeck And Desmos Geometric Transformations Absolute Value Summer Math

Lesson Function Transformations Translations Nagwa

Dynamic Transformations Using Peardeck And Desmos Geometric Transformations Absolute Value Summer Math
Comments
Post a Comment